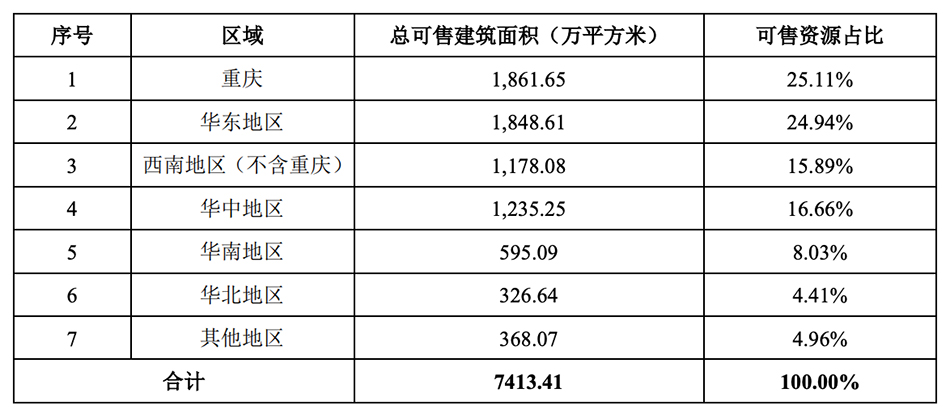
圆锥曲线之抛物线定义及其方程推导! 抛物线顶点公式
抛物线顶点公式(圆锥曲线之抛物线定义及其方程推导)
抛物线定义形如下列表达情势的函数

文章插图
它是一个二次多项式函数,其图像是一条抛物线,我们很容易求出它的对称轴和定点坐标 。除了对称性之外资源网,抛物线还有那些几何性质呢?
其实抛物线的精确定义为,平面中到一个定点F和一条肯定的直线l(F不在l上)的距离雷同的点形成的轨迹 。其中点F为抛物线的焦点,直线l为抛物线的准线 。
抛物线方程推导为了简便起见,我们仍然将抛物线的对称轴定为坐标轴,顶点为原点 。下面我们依据抛物线的性质来推导其方程 。
【圆锥曲线之抛物线定义及其方程推导! 抛物线顶点公式】

文章插图
若抛物线资源网的焦点坐标为F(p/2,0),准线方程为x=-p/2,假设抛物线上任意一点的坐标为(x,y),那么有下列等式成立

文章插图
这就是关于x轴对称、定点在原点的抛物线方程 。当p为正实数时,x为非负值,即抛物线的启齿方向为x轴正方向;资源网当p为负实数时,x为非正值,即抛物线的启齿方向为x轴负方向 。
推荐阅读
- 刘镇伟|1981年的《凶榜》:琼瑶御用小生的转型之作,女主角连遭意外早逝
- 蔡少芬|婚后力捧老公上位,这6位女明星个个不简单,复出之后依旧是女神
- 郭靖杨过谁是侠之大者,乔峰和郭靖谁是第一大侠-
- 吃中药可以吃豆腐吗?
- 八拜之交的历史典故,什么是八拜之交典故都是什么-
- 洗浴王之洗澡的正确顺序 洗澡顺序
- 理想与梦想之间的区别,梦想跟理想区别-
- 很少有人翻唱周深的歌,歌手当打之年周深被谁奇袭-
- 关之琳|关之琳:未修图近照眼里充满沧桑,卖掉上亿珠宝可能是缺钱
- 赵丽颖|终于来了!《心之所向》官宣,谭松韵主演,光预告片就连刷三遍