з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ3пјү
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жң¬ж–ҮжҳҜгҖҢеҠЁжҖҒ规еҲ’гҖҚзі»еҲ—ж–Үз« зҡ„第дёүзҜҮ пјҢ дҪңдёә з®—жі•иҗҢж–°еҰӮдҪ•еӯҰеҘҪеҠЁжҖҒ规еҲ’пјҲ2пјү зҡ„дёҖдёӘ延伸 гҖӮ жң¬зҜҮж–Үз« е°Ҷдё»иҰҒиҒҡз„ҰдәҺеҠЁжҖҒ规еҲ’з»Ҹе…ёжЁЎеһӢ вҖ”вҖ” иғҢеҢ…й—®йўҳзҡ„и®Іи§Ј гҖӮ
иғҢеҢ…й—®йўҳеұһдәҺзәҝжҖ§ DP жЁЎеһӢ пјҢ д№ӢжүҖд»ҘеҚ•зӢ¬жӢҺеҮәжқҘи®І пјҢ дё»иҰҒжҳҜеӣ дёәиҜҘй—®йўҳдҝЎжҒҜйҮҸеӨ§дё”еҚҒеҲҶйҮҚиҰҒ пјҢ еұһдәҺйқўиҜ•дёӯеёёиҖғдё”еҝ…дјҡзҡ„зҹҘиҜҶ пјҢ еӣ жӯӨжҲ‘们е°Ҷе…¶ж”ҫеңЁжң¬зі»еҲ—зҡ„第дёүзҜҮиҝӣиЎҢд»Ӣз»Қ гҖӮ
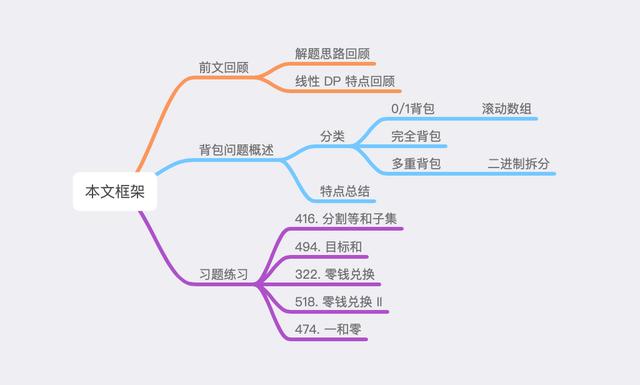
жң¬ж–ҮдёҖе…ұеҲҶдёәдёүдёӘйғЁеҲҶ пјҢ е…·дҪ“еҶ…е®№жЎҶжһ¶еҰӮдёӢжүҖзӨәпјҡ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
еүҚж–ҮеӣһйЎҫи§ЈйўҳжҖқи·ҜеӣһйЎҫеӣһйЎҫеҠЁжҖҒ规еҲ’зі»еҲ—зҡ„第дёҖзҜҮж–Үз« пјҢ еҠЁжҖҒ规еҲ’и§ЈйўҳиҝҮзЁӢдёҖе…ұеҲҶдёәдёӨжӯҘ пјҢ дёҖжҳҜзЎ®е®ҡгҖҢDP зҠ¶жҖҒгҖҚ пјҢ дәҢжҳҜзЎ®е®ҡгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚ гҖӮ
гҖҢDP зҠ¶жҖҒгҖҚзҡ„зЎ®е®ҡжңүдёӨеӨ§еҺҹеҲҷ пјҢ дёҖжҳҜгҖҢжңҖдјҳеӯҗз»“жһ„гҖҚ пјҢ дәҢжҳҜгҖҢж— еҗҺж•ҲжҖ§гҖҚ пјҢ з®ҖиҰҒжҰӮжӢ¬е°ұжҳҜе°ҶеҺҹй—®йўҳеҲ’еҲҶдёәеӨҡдёӘеӯҗй—®йўҳ пјҢ дё”гҖҢеӨ§и§„жЁЎеӯҗй—®йўҳжңҖдјҳеҖјгҖҚд»…дёҺгҖҢе°Ҹ规模еӯҗй—®йўҳжңҖдјҳеҖјгҖҚжңүе…і пјҢ дёҺгҖҢе°Ҹ规模еӯҗй—®йўҳжңҖдјҳеҖјгҖҚжҳҜеҰӮдҪ•еҫ—еҲ°зҡ„ж— е…і гҖӮ
жӯӨеӨ„зҡ„гҖҢеӨ§и§„жЁЎгҖҚдёҺгҖҢе°Ҹ规模гҖҚ пјҢ е°ұжҳҜгҖҢDP й—®йўҳгҖҚзҡ„е…ій”®жүҖеңЁ пјҢ д№ҹжҳҜ DP й—®йўҳеҲҶзұ»зҡ„йҮҚиҰҒж ҮеҮҶ гҖӮ
зЎ®е®ҡе®ҢгҖҢDP зҠ¶жҖҒгҖҚеҗҺ пјҢ еҸӘйңҖиҰҒеҲҶзұ»и®Ёи®әгҖҒз»Ҷеҝғжһҡдёҫеҗ„з§Қжғ…еҶө пјҢ еҚіеҸҜеҫ—еҲ°гҖҢDP иҪ¬з§»ж–№зЁӢгҖҚ гҖӮ
еӨ§е®¶еңЁзңӢжң¬ж–Үж—¶ пјҢ дёҖе®ҡиҰҒз»ҶеҝғдҪ“дјҡжҜҸдёҖдёӘз»Ҹе…ёиғҢеҢ…жЁЎеһӢзҡ„гҖҢDP зҠ¶жҖҒгҖҚдёҺгҖҢDP иҪ¬з§»ж–№зЁӢгҖҚ пјҢ и®ӨзңҹжҖқиҖғжҜҸдёҖдёӘжЁЎеһӢдёӯиҝҷдёӨйғЁеҲҶжҳҜеҰӮдҪ•еҫ—еҲ°зҡ„ гҖӮ еӯҰд№ дёҚеҗҢз»Ҹе…ёжЁЎеһӢ пјҢ зҗҶи§ЈжЁЎеһӢжң¬иҙЁ пјҢ жүҚиғҪдёҚж–ӯеҠ ж·ұеҜ№гҖҢеҠЁжҖҒ规еҲ’гҖҚй—®йўҳзҡ„зҗҶи§Ј гҖӮ
зәҝжҖ§ DP зү№зӮ№еӣһйЎҫзәҝжҖ§еҲ’еҲҶ DP 规模зҡ„еҠЁжҖҒ规еҲ’з®—жі•иў«з»ҹз§°дёәзәҝжҖ§ DP гҖӮ еңЁзәҝжҖ§ DP дёӯ пјҢ DP зҠ¶жҖҒд»ҺгҖҢе°Ҹ规模гҖҚиҪ¬з§»еҲ°гҖҢеӨ§и§„жЁЎгҖҚзҡ„еҗҢж—¶ пјҢ DP зҠ¶жҖҒжІҝзқҖеҗ„дёӘз»ҙеәҰзәҝжҖ§еўһй•ҝ гҖӮ
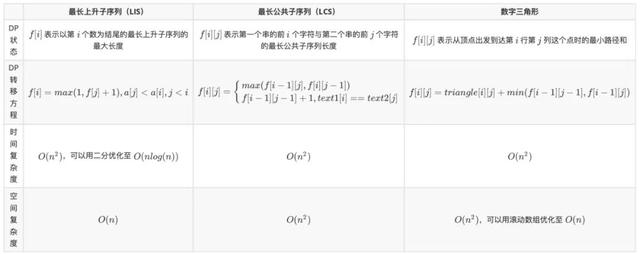
жҲ‘们еңЁеҠЁжҖҒ规еҲ’зі»еҲ—зҡ„第дәҢзҜҮж–Үз« дёӯд»Ӣз»ҚдәҶдёүдёӘеёёи§Ғзҡ„зәҝжҖ§ DP жЁЎеһӢ пјҢ еҲҶеҲ«жҳҜгҖҢжңҖй•ҝдёҠеҚҮеӯҗеәҸеҲ— LISгҖҚгҖҒгҖҢжңҖй•ҝе…¬е…ұеӯҗеәҸеҲ— LCSгҖҚд»ҘеҸҠгҖҢж•°еӯ—дёүи§’еҪўгҖҚ пјҢ е…¶зү№зӮ№еҰӮдёӢеӣҫжүҖзӨә гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
жң¬ж–Үе°Ҷд»Ӣз»Қ第еӣӣдёӘзәҝжҖ§ DP жЁЎеһӢ пјҢ еҚігҖҢиғҢеҢ…й—®йўҳгҖҚ гҖӮ з”ұдәҺиғҢеҢ…й—®йўҳд№ҹжҳҜзәҝжҖ§ DP й—®йўҳ пјҢ еӣ жӯӨд№ҹз¬ҰеҗҲзәҝжҖ§ DP зҡ„зү№зӮ№ пјҢ еҚі DP зҠ¶жҖҒжІҝзқҖеҗ„дёӘз»ҙеәҰзәҝжҖ§еўһй•ҝ пјҢ еӨ§е®¶еҸҜд»ҘеңЁдёӢж–ҮдёӯзқҖйҮҚе…іжіЁдёҖдёӢиҝҷдёҖзү№зӮ№ гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иғҢеҢ…й—®йўҳжҰӮиҝ°еёёи§Ғзҡ„иғҢеҢ…й—®йўҳдёҖе…ұжңүдёүзұ» пјҢ еҲҶеҲ«жҳҜгҖҢ0/1 иғҢеҢ…гҖҚгҖҒгҖҢе®Ңе…ЁиғҢеҢ…гҖҚд»ҘеҸҠгҖҢеӨҡйҮҚиғҢеҢ…гҖҚ пјҢ жҺҘдёӢжқҘжҲ‘们е°Ҷдҫқж¬ЎиҝӣиЎҢд»Ӣз»Қ гҖӮ
0/1 иғҢеҢ…0/1 иғҢеҢ…зҡ„еҹәжң¬жЁЎеһӢеҰӮдёӢжүҖзӨәпјҡ
дёҖе…ұжңү N дёӘзү©е“Ғ пјҢ е…¶дёӯ第 i дёӘзү©е“Ғзҡ„дҪ“з§Ҝдёә
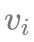 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ д»·еҖјдёә
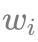 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
гҖӮ зҺ°иҰҒжұӮйҖүжӢ©дёҖдәӣзү©е“Ғж”ҫе…ҘдёҖдёӘе®№з§Ҝдёә M зҡ„иғҢеҢ…дёӯ пјҢ дҪҝеҫ—зү©е“ҒжҖ»дҪ“з§ҜдёҚи¶…иҝҮ M зҡ„еүҚжҸҗдёӢ пјҢ зү©е“ҒжҖ»д»·еҖјжңҖеӨ§ гҖӮ
зҺ°еңЁжҲ‘们жқҘжҖқиҖғдёӢеҰӮдҪ•ж №жҚ®зәҝжҖ§ DP зҡ„зҹҘиҜҶжқҘи§ЈеҶіиҝҷдёӘй—®йўҳ гҖӮ
зәҝжҖ§ DP зҡ„зү№зӮ№жҳҜ DP зҠ¶жҖҒжІҝзқҖеҗ„дёӘз»ҙеәҰзәҝжҖ§еўһй•ҝ гҖӮ иҖҢжң¬й—®йўҳдёӯеҸӘжңүдёүдёӘеҸӮж•° пјҢ еҲҶеҲ«жҳҜзү©е“Ғзј–еҸ·гҖҒзү©е“ҒдҪ“з§Ҝд»ҘеҸҠзү©е“Ғд»·еҖј гҖӮ з”ұдәҺжҲ‘们иҰҒжұӮзҡ„жҳҜзү©е“ҒжҖ»д»·еҖјжңҖеӨ§ пјҢ еӣ жӯӨдёҚйҡҫжғіеҲ°д»Ө DP зҠ¶жҖҒдёә
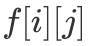 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
пјҢ иЎЁзӨәд»…иҖғиҷ‘еүҚ i дёӘзү©е“Ғ пјҢ жүҖйҖүзү©е“ҒжҖ»дҪ“з§Ҝдёә j ж—¶зҡ„жңҖеӨ§зү©е“ҒжҖ»д»·еҖј гҖӮ
жҺЁиҚҗйҳ…иҜ»
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- еҗ‘ж—Ҙи‘өиҝңзЁӢжҺ§еҲ¶дјҒдёҡзүҲе®ўжҲ·з«Ҝжӣҙж–°еҚҮзә§пјҢдјҳеҢ–иҝңжҺ§UIйҖӮй…ҚSADDCеҶ…ж ёз®—жі•
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- иҷҫзұійҹід№җе®Јеёғе…іеҒңпјҒжҲ‘зҡ„жӯҢеҚ•еҰӮдҪ•еҜје…ҘQQйҹід№җгҖҒзҪ‘жҳ“дә‘йҹід№җпјҹ
- дәәи„ёиҜҶеҲ«и®ҫеӨҮдё»жқҝеҰӮдҪ•йҖүеһӢ иҪҜзЎ¬ж•ҙеҗҲеӨ§е№…зј©зҹӯејҖеҸ‘ж—¶й—ҙ
- Mini-LEDдә§е“Ғж•Ҳжһң究з«ҹеҰӮдҪ•пјҹ
- 专家д»Ӣз»ҚеҰӮдҪ•еҲӨж–ӯжҷәиғҪжүӢжңәиў«е…ҘдҫөпјҡиҝҗиЎҢйҖҹеәҰеҸҳж…ўгҖҒз”өжұ ж¶ҲиҖ—иҝҮеҝ«д»ҘеҸҠеҚЎйЎҝ
- еңЁи°·жӯҢз®—жі•жӣҙж–°д№ӢеҗҺ2020е№ҙзӣ—зүҲзҪ‘з«ҷжөҒйҮҸй”җеҮҸдёүеҲҶд№ӢдёҖ















