江苏龙网

  1. 首页 > 资讯 > 科技 > >

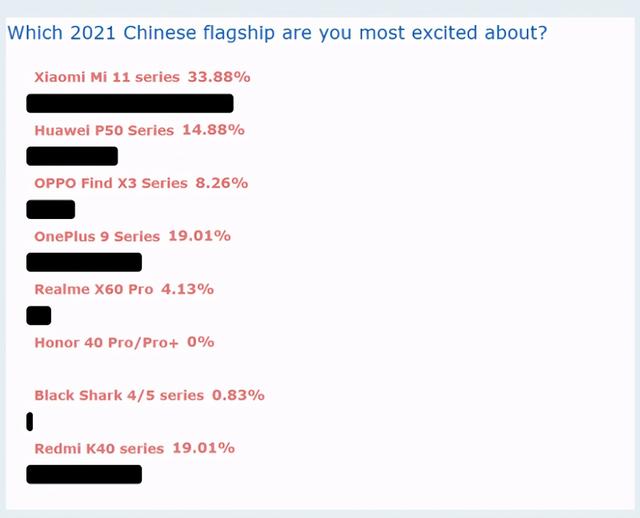
|三辩三驳：这篇论文告诉你传统优化分析与现代DL有哪些不匹配


编辑：小舟、陈萍
你的学习率的大小调合适了吗？
|三辩三驳：这篇论文告诉你传统优化分析与现代DL有哪些不匹配
本文插图

从事机器学习方面相关研究的人都了解 ， 网络模型的最终性能少不了优化 。 其中损失函数扮演了非常重要的角色 ， 而随机梯度下降算法（SGD）由于其良好的收敛性 ， 常常被用来进行梯度更新 。 为了加快收敛速度 ， 缩短训练时间 ， 同时为了提高求解精度 ， 采用随机梯度下降算法应该注意学习率（Learning Rate, LR）等参数的调整 。 那么 LR 的大小对现代深度学习与传统优化分析的是怎样的呢？下面通过一篇论文进行解答 。
该论文就是《Reconciling Modern Deep Learning with Traditional Optimization Analyses: The Intrinsic Learning Rate》 ， 指出了归一化网络与传统分析之间的不兼容性 。 在深入研究这些结果之前 ， 先回顾一下权重衰减（又名ξ2 正则化）训练归一化网络 。 则随机梯度下降 (SGD) 的第 t 次迭代为：
|三辩三驳：这篇论文告诉你传统优化分析与现代DL有哪些不匹配
本文插图

λ表示权重衰减 (WD) 因子（或者?2 - 正则化系数） ， ηt 表示学习率 ， Bt 表示 batch ， ?L(wt,Bt)表示 batch 梯度 。
在比较理想的假设下（即在随机初始化期间固定顶层不会影响最终准确度） ， 用于训练此类归一化网络的损失函数尺度不变 ， 这意味着 L（wt ; Bt）=L（cwt ; Bt）, ?c>0 。
尺度不变性的结果就是：对于任意 c>0 ， ?wL|w=w0=c?wL|w=cw0 以及?2wL|w=w0=c2?2wL|w=cw0 。
传统观点（Conventional Wisdom, CW）
CW1：当 LR 降至零时 ， 优化动态收敛到一条确定的路径（梯度流） ， 沿着该路径训练损失显著减小 。
回想一下 ， 在解释传统（确定）梯度下降中 ， 如果 LR 小于损失函数平滑度的倒数 ， 那么每一步都会减少损失 。 SGD 是随机的 ， 在可能的路径上都有分布 。 但是 ， 极小的 LR 可以看作是 full-batch 梯度下降（GD） ， 它在无穷小的步长范围内接近梯度流（GF） 。
上述推理表明 ， 极小的 LR 至少可以减少损失 ， 那么更高的 LR 也可以 。 当然 ， 在深度学习中 ， 我们不仅关注优化 ， 还关注泛化 。 在这里小的 LR 是有危害的 。
CW2：为达到最好的泛化能力 ， LR 在几个 epoch 之后必须迅速地变大 。
这是一个经验发现：从一开始使用太小的学习率或太大的批量（所有其他超参数固定）会导致更糟糕的泛化 。
对这种现象的一个普遍解释是 ， 在 SGD 过程中梯度估计中的噪声有利于泛化（如前所述 ， 当 LR 非常小的时候 ， 这种噪声会趋于平均） 。 许多研究者认为 ， 噪声之所以有帮助 ， 是因为它使轨迹远离尖锐极小值（sharp minima） ， 而这些极小值让泛化变得更差 ， 尽管这里有一些不同的意见 。
Yuanzhi Li 等人在论文《Towards Explaining the Regularization Effect of Initial Large Learning Rate in Training Neural Networks》中给出一个示例 ， 一个简单的双层网络 。 其中 ， 由于 LR 小而导致的泛化结果更差在数学上得到了证明 ， 同时也得到了实验验证 。
CW3：用随机微分方程（Stochastic Differential Equation, SDE）在固定高斯噪声的连续时间内对 SGD 进行建模 。 也就是说 ， 可以把 SGD 看做是一个扩散过程 ， 它在训练过的网络上混合一些类吉布斯（Gibbs-like）分布 。
SGD 是带有噪声项的梯度下降 ， 它具有的连续时间近似可以描述为以下扩散过程：
|三辩三驳：这篇论文告诉你传统优化分析与现代DL有哪些不匹配
本文插图

其中 ， σWt 为随机梯度?L(Wt;Bt)的协方差 ， Bt 为适当维数的布朗运动（Brownian motion） 。 一些研究采用了 SDE 观点 ， 对噪声的影响进行了严格的分析 。


推荐阅读


上一篇：|华为商标被“抢注”？亮风台内部人士：并非恶意抢注，已经在协商解决

下一篇：|创新未必要“硬来”看柔宇以柔克刚的源创新之路