江苏龙网

  1. 首页 > 人文 > >

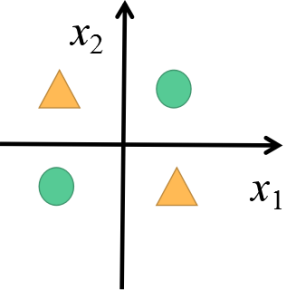
|感知机实现非线性分类

|感知机实现非线性分类

文章图片

|感知机实现非线性分类

文章图片

|感知机实现非线性分类

文章图片

|感知机实现非线性分类

文章图片

|感知机实现非线性分类

文章图片


感知机实现非线性分类
在上回故事中 ， 我们谈到了由单个神经元所构成的感知机无法处理非线性分类问题 。 如图1所示 。

图1 非线性分类数据
对于单个神经元（两输入 ， 单输出）所构成的感知机 ， 其分类边界为：w1x1+w2x2+b=0 ， 从其分类边界也可以发现 ， 它只能处理线性可分的数据 。
那么 ， 当遇到如图1所示的线性不可分数据应该怎么办呢？
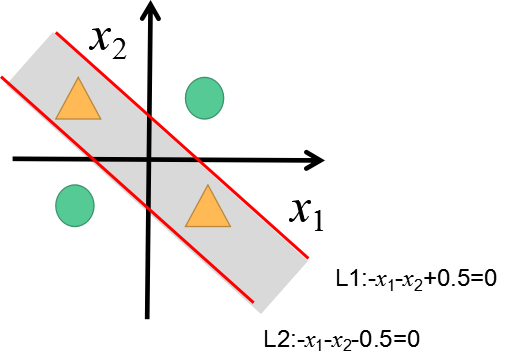
在上一回中 ， 我们提到了可以通过构建类似图2的分类边界来实现非线性数据的分类 。 那么 ， 我们应该如何来设计我们的神经元结构呢？

图2 非线性数据分类
首先 ， 我们可以发现 ， 图2所示的边界由两条直线组成 ， 且对于图2所示的数据 ， 输入维度为2 ， 输出维度为1 。 在这里 ， 我们假设黄色的三角形为第0类数据 ， 绿色的圆形为第1类数据 。 因此 ， 我们可以确定我们的神经元结构输入维度为2 ， 输出维度为1 。 最终设计的感知机结构如图3所示 。 在图3所示的结构中 ， 该结构接受两个输入 ， 一个输出 ， 在第一层的结构中 ， 我们设计了两个神经元 ， 希望这两个神经元能够分别模拟两个直线分类边界 ， 因为我们最终的输出为一个维度 ， 所以在第一层神经元的基础上再添加了一个神经元 ， 该神经元的作用就是将1号及2号神经元的输出进行联合 ， 即实现图2中的阴影部分的功能 。

图3 感知机实现非线性分类
为简单起见 ， 在这里 ， 我们假设已知这两条直线的方程 ， 如图4所示 。

图4 边界方程
根据L1与L2 ， 可将图3中感知机的1号神经元与2号神经元权重及偏置项分配为：

图5 1号与2号神经元的权重及偏置项分配
接下来 ， 让我们看看 ， 对于图2中所示数据 ， 1号与2号神经元的输出经过激活函数（这里激活函数选择与之前章节一致）后的输出：

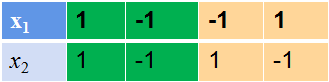
图6 1号与2号神经元输出 ， 及其经过激活函数后的输出
图6中 ， 括号外的数据为神经元输出 ， 括号内的数据为神经元输出经过激活函数后的输出 ， 现在 ， 我们将图6画出来 ， 如图7所示：

图7 神经元输出经过激活函数后的输出可视化结果
如图7所示 ， 我们的输入在经过1号神经元与2号神经元后的输出映射为了线性可分的数据 ， 我们可以寻找到如图7中L3所示的边界将这两类输出数据区分开 ， 即我们可以将3号神经元权重及偏执设置为：

图7 3号神经元权重及偏置项设置
现在让我们来检测下图7所示的多个神经元构成的感知机结构是否能够将图2所示的数据区分开 ， 如图8所示：

图8 神经网络功能验证
如图8中3号神经元的输出经过激活函数映射后的输出所示 ， 对于图1中所示的数据 ， 该结构可以将其完美地区分开 。
【|感知机实现非线性分类】最后 ， 总结一下 ， 我们在该结构设计过程中 ， 对于1号及2号神经元 ， 其实是我们从自己的视角出发 ， 已经假定了L1与L2已知 ， 在这个基础上才有L3的设计过程 。 但实际情况下 ， 我们是不知道L1与L2的？这种情况下 ， 我们又应该如何求取L1与L2呢？欲知后事如何 ， 请听下回分解！


    推荐阅读


    上一篇：为何男人，在婚外感情中，更钟情于已婚女人

    下一篇：东方网|龚正当选上海市市长