江苏龙网

  1. 首页 > 生活 > >

函数|高考数学易考的62个高频考点！出题人再厉害也逃不开( 二 )


例题：已知函数f(x)=ax 3 -3x 2 +1,若f(x)存在唯一的零点x 0 ,且x 0 ＞0 ， 则a的取值范围为：
A、（2 ， +∞） B、（-∞ ， -2） C、（1 ， +∞） D、（-∞ ， -1）
解析：取a=3,f(x)=3x 3 -3x 2 +1 ， 不合题意 ， 可以排除A与C；取a=-4/3,f(x)=-4x 3 /3-3x 2 +1 ， 不合题意 ， 可以排除D；故只能选B
2
特例法
有些选择题涉及的数学问题具有一般性 ， 这类选择题要严格推证比较困难 ， 此时不妨从一般性问题转化到特殊性问题上来 ， 通过取适合条件的特殊值、特殊图形、特殊位置等进行分析 ， 往往能简缩思维过程、降低难度而迅速得解 。
例题：2016年高考全国卷Ⅱ理数第12题
已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=x+1/x与y=f(x)图像焦点为为（x 1 ,y 1 ),(x 2 ,y 2 ),… ， （x m ,y m ),则∑ m i=1 （x i +y i ）=（ ）
A、0 B、m C、2m D、4m
解析：由f(-x)=2-f(x)得 ， f(x)关于（0,1）对称 ， 故可取符合题意的特殊函数f(x)=x+1,联立y=x+1,y=x+1/x,解得交点为（-1,0）和（1,2） ， 所以∑ 2 i=1 （x i +y i ）=（x 1 +y 1 )+(x 2 +y 2 )=（-1+0）+（1+2）=2 ， 此m=2 ， 只有选项B符合题意 。
3
极限法
当一个变量无限接近一个定量 ， 则变量可看作此定量 。 对于某些选择题 ， 若能恰当运用极限法 ， 则往往可使过程简单明快 。
例题：对任意θ∈（0 ， π/2）都有（ ）
A sin(sinθ)<cosθ<cos(cosθ)
B sin(sinθ)>cosθ>cos(cosθ)
C sin(cosθ)<cos(sinθ)<cosθ
D sin(cosθ)<cosθ<cos(sinθ)
解析：当θ→0时 ， sin(sinθ)→0 ， cosθ→1 ， cos(cosθ)→cos1 ， 故排除A与B；当θ→π/2时 ， cos(sinθ)→cos1 ， cosθ→0 ， 故排除C ， 只能选D 。
函数|高考数学易考的62个高频考点！出题人再厉害也逃不开
文章图片

【函数|高考数学易考的62个高频考点！出题人再厉害也逃不开】1
特殊化法
当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时 ， 而已知条件中含有某些不确定的量 ， 可以将题中变化的不定量选取一些符合条件的恰当特殊值（或特殊函数 ， 或特殊角 ， 图形特殊位置 ， 特殊点 ， 特殊方程 ， 特殊模型等）进行处理 ， 从而得出探求的结论 。 这样可大大地简化推理、论证的过程 。
例题：
如图 ， 设F 1 F 2 为椭圆x 2 /100+y 2 /64=1的两个焦点 ， P在椭圆上 ， I为△PF1F2的内心 ， 直线PI交长轴于Q ， 则I分PQ所成的比为：
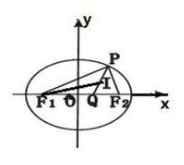
函数|高考数学易考的62个高频考点！出题人再厉害也逃不开
文章图片

解析：将点P与短轴上端点B重合 ， 则在直角△BF 1 O中 ， |F 1 B|=a=10,|F 1 O|=c=6,因为F 1 I平分角BF 1 O ， 所以BI/IO=|F 1 B|/|F 1 B|=10/6=5/3,即I分PQ所成的比为5/3
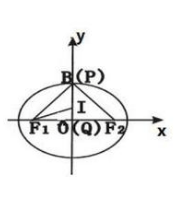
函数|高考数学易考的62个高频考点！出题人再厉害也逃不开
文章图片

2
数形结合法
将抽象、复杂的数量关系 ， 通过图像直观揭示出来 。 对于一些含有几何背景的填空题 ， 若能数中思形 ， 以形助数 ， 则往往可以简捷地解决问题 ， 得出正确的结果 。
例题：
已知双曲线C：x 2 /a 2 -y 2 /b 2 =1(a>0,b>0)的右顶点为A ， 以A为圆心 ， b为半径作圆 ， 圆A与双曲线C的一条渐近线交于M,N两点 ， 若∠MAN为60度 ， 则C的离心率为：
解析：作AP⊥MN ， 因为圆A与双曲线C的一条渐近线交于M,N两点 ， 则MN为双曲线的渐近线y=bx/a上的点 ， 且A（a,0）,|AM|=|AN|=b,AP⊥MN,所以∠PAN为30度 ， 点A（a,0）到直线y=bx/a的距离|AP|=|b|/√(1+b 2 /a 2 ),在Rt△PAN中 ， cos∠PAN=|PA|/|NA|,代入计算得a 2 =3b 2 ,c=2b,所以e=c/a=2√3/3


推荐阅读


上一篇：范冰冰|刚传出与前男友复合，就立刻开始秀恩爱，“范爷”这波操作神了

下一篇：财经类|热门专业中的香饽饽：30所财经类热门院校及专业实力盘点！