Type theoryйҮҢзҡ„coinductionжҖҺж ·зҗҶи§Ј
structural induction иғҪз”ЁжқҘиҜҒжҳҺ lambda calculus (д№ҹз®—жҳҜ infinite data structure еҗ§) зҡ„е®ҡзҗҶгҖӮ гҖҗType theoryйҮҢзҡ„coinductionжҖҺж ·зҗҶи§ЈгҖ‘ д»ҺиҝҷеҸҘиҜқеҸҜд»ҘзңӢеҮәйўҳдё»еҜ№ inductionпјҲжҲ–иҖ…иҜҙ lambda calculusпјүзҡ„зҗҶи§Јжңүй—®йўҳгҖӮstructural induction еҸҜд»ҘзҗҶи§ЈдёәгҖҗеҜ№дәҺд»»ж„ҸеӨ§е°Ҹзҡ„ж•°жҚ®пјҢжҲ‘们еҸҜд»ҘеҪ’зәіе®ҡд№үе®ғдёҠйқўзҡ„иҝҗз®—гҖ‘пјҢжіЁж„ҸиҝҷйҮҢжҳҜгҖҗеҜ№дәҺд»»ж„ҸеӨ§е°Ҹзҡ„гҖ‘вҖ”вҖ”гҖҗеҜ№дәҺд»»ж„ҸгҖ‘жҳҜеӣ дёәдҪ зҡ„еҮҪж•°жҳҜ total зҡ„гҖӮиҝҷ并дёҚж„Ҹе‘ізқҖж•°жҚ®зҡ„ж— йҷҗдёҺжңүйҷҗпјҢеӣ дёә induction еҸӘжҳҜи§Јжһ„зҡ„ж–№ејҸпјҢиҖҢдҪ еңЁжһ„йҖ зҡ„ж—¶еҖҷеҸӘиғҪжһ„йҖ еҮәжңүйҷҗеӨ§е°Ҹзҡ„ж•°жҚ®пјҲиҝҷжҳҜеӣ дёәжңү termination checkгҖӮжҲ–иҖ…иҜҙдҪ дҪҝз”Ё eliminator зҡ„ж—¶еҖҷе°ұдёҚеҸҜиғҪеӯҳеңЁж— йҷҗзҡ„йҖ’еҪ’пјүгҖӮдёҫдёӘдҫӢеӯҗпјҢз»ҷе®ҡдёҖдёӘз”ұZeroе’ҢSuccдёӨдёӘжһ„йҖ еҷЁдә§з”ҹзҡ„дёҖиҝӣеҲ¶иҮӘ然数пјҢдҪ еҶҷдёҚеҮәиҝҷж ·зҡ„д»Јз Ғпјҡmugen = Succ mugenеӣ дёәдҪ дёҚиғҪж— йҷҗең°йҖ’еҪ’жһ„йҖ гҖӮжіЁж„ҸжҲ‘们зҺ°еңЁжІЎжңүи®Ёи®ә inductionпјҢиҖҢжҳҜеңЁи®Ёи®әжһ„йҖ гҖӮ
иҖҢеҒҮи®ҫжҲ‘们зҡ„иҮӘ然数зұ»еһӢжҳҜ coinductive зҡ„пјҢдҪ е°ұиғҪеӨҹеҶҷеҮәдёҠйқўйӮЈж ·зҡ„д»Јз ҒпјҢиҖҢдё”дҪ еҶҷеҮәзҡ„д»»дҪ•дёҖдёӘгҖҗжһ„йҖ гҖ‘иҮӘ然数зҡ„еҮҪж•°пјҢйғҪеҝ…йЎ»еңЁиў«и§Јжһ„жҲҗжӣҙе°ҸйғЁеҲҶж—¶пјҢйҖ’еҪ’и°ғз”ЁиҮӘе·ұпјҲиҖҢеңЁ induction йҮҢйқўпјҢдҪ жҳҜгҖҗеңЁжһ„йҖ жӣҙеӨ§зҡ„дёңиҘҝж—¶пјҢйҖ’еҪ’и°ғз”ЁиҮӘе·ұгҖ‘пјүгҖӮ
в– зҪ‘еҸӢ
жҳЁеӨ©еҲҡеҲҡеҗ¬дәҶPеӨ§иғЎжҢҜжұҹиҖҒеёҲзҡ„PLиҜҫи®Іrecursive typeд»ҠеӨ©е°ұзңӢеҲ°дәҶиҝҷдёӘй—®йўҳпјҢдёӢйқўжқҘеӢүејәеӣһзӯ”дёҖдёӢгҖӮ
йҰ–е…ҲпјҢжҲ‘и§үеҫ—structural inductionзҡ„жң¬иҙЁд№ҹжҳҜTaPLиҝҷжң¬д№ҰдёҠ284йЎөзҡ„principle of induction:
пјҢеӣ жӯӨз”Ёinductionж–№жі•иҜҒжҳҺзҡ„lambda calculusзҡ„жҖ§иҙЁйғҪжҳҜжңүз©·ж¬Ўеә”з”Ёlambda calculusзҡ„syntax ruleеҫ—еҲ°зҡ„иЎЁиҫҫејҸгҖӮ
иҮідәҺжҖҺд№ҲзҗҶи§Јco-inductionпјҢеҸҜд»Ҙе…ҲиҖғиҷ‘иҖғиҷ‘жҖҺд№ҲзҗҶи§ЈinductionпјҢиҝҷдёӨдёӘжҰӮеҝөд№Ӣй—ҙзҡ„е…іиҒ”жҖ§йқһеёёејәпјҢиҖҢеӣ дёәеңЁй«ҳдёӯдҫҝзҶҹзҹҘеҗ„з§ҚеҪ’зәіжі•пјҢдҪҝеҫ—inductionеңЁжҲ‘们зҡ„еӨ§и„‘йҮҢе…Ҳе…Ҙдёәдё»пјҢд»ҺиҖҢдёҚжҳҜеҫҲеҘҪжҺҘ收co-inductionзҡ„жҰӮеҝөгҖӮд»ҘTaPLдёӯrecursive typeиҝҷдёҖз« зҡ„subtyping relationдёәдҫӢпјҢд№Ұдёӯз»ҷеҮәзҡ„е®ҡд№үжҳҜпјҡ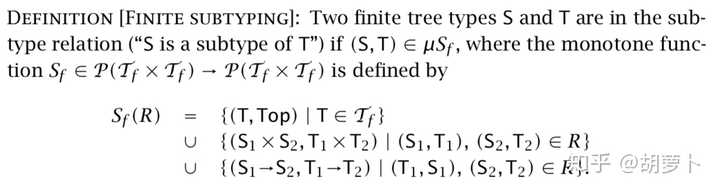

еҸҜд»ҘзңӢеҲ°generating functionзҡ„еҪўејҸеҹәжң¬дёҖиҮҙпјҢиҖҢдё”ж №жҚ®generating functionеҶҷеҮәзҡ„inference ruleд№ҹжҳҜе®Ңе…ЁдёҖж ·зҡ„гҖӮдёҚеҗҢд№ӢеӨ„еңЁдәҺпјҡfinite subtypingе…ізі»йӣҶеҗҲйҖҡиҝҮеҸ–generating functionзҡ„жңҖе°ҸдёҚеҠЁзӮ№еҫ—еҲ°пјҢеҸ«еҒҡinductively definedпјӣinfinite subtypingе…ізі»йӣҶеҗҲйҖҡиҝҮеҸ–generating functionзҡ„жңҖеӨ§дёҚеҠЁзӮ№еҫ—еҲ°пјҢеҸ«еҒҡco-inductively definedгҖӮinductiveжҳҜжһ„йҖ жҖ§зҡ„пјҢжҜ”еҰӮжҲ‘еҸҜд»Ҙз”ұ
жҳҜ
зҡ„еӯҗзұ»е’Ң
жҳҜ
зҡ„еӯҗзұ»жһ„йҖ еҮә
жҳҜ
зҡ„еӯҗзұ»пјҢиҝҷж ·жһ„йҖ зҡ„з»“жһңдёҚдјҡеҢ…еҗ«ж— з©·ж•°жҚ®зұ»еһӢпјӣиҖҢco-inductiveжҳҜdeconstructзҡ„пјҢдёҺжһ„йҖ зҡ„иҝҮзЁӢеҲҡеҘҪзӣёеҸҚпјҢеҸҜд»ҘзҗҶи§ЈдҪңвҖңи§ӮеҜҹжҖ§вҖқзҡ„пјҢжҲ‘еҸҜд»ҘзӣҙжҺҘи§ӮеҜҹеҲ°
жҳҜ
зҡ„еӯҗзұ»пјҢе…¶дёӯ
е’Ң
жҺЁиҚҗйҳ…иҜ»
- иҫ№еҹҺж»ЎжҙІйҮҢпјҢеҶ¬ж—ҘйҮҢзҡ„жё©жҡ–
- жұҪиҪҰзҹҘиҜҶ|еҶ¬ж—ҘйҮҢзҡ„иҝҪе…үиҖ…вҖ”вҖ”иҜә马иҝӘжЈ®вҖңеҫҒйҖ”иҖ…BвҖқ
- иҪ®иғҺ|жҡ–жҡ–зҡ„еҶ¬ж—ҘпјҢжғіе’ҢиҝҷйҮҢзҡ„иҠұе„ҝдёҖиө·жҖ’ж”ҫпјҒ
- |йӮўеҸ°иҪҰдё»еҸҚжҳ пјҡиЎҢ驶йҮҢзЁӢ2600е…¬йҮҢзҡ„ж–°иҪҰпјҢз§Ҝзўіз«ҹеғҸи·‘дәҶ10дёҮе…¬йҮҢ
- жҖҺд№Ҳж ·е°Ҷ家йҮҢзҡ„ж¶Іжҷ¶з”өи§Ҷе’Ң笔记жң¬з”өи„‘иҝһжҺҘ
- жұҪиҪҰзҹҘиҜҶ|вҖңеӨ§дә”еә§вҖқSUVйҮҢзҡ„жқ°еҮәд»ЈиЎЁ е®һжӢҚжң¬з”°UR-V
- жҖқеҹҹ|2022ж¬ҫжң¬з”°жҖқеҹҹType Rи·ҜиҜ•и°Қз…§пјҢеӨҡеӨ„жҗӯиҪҪиҝҗеҠЁеҘ—件
- |е…ЁзҪ‘еҘҪиҜ„зҡ„еҗүеҲ©жҳҹз‘һпјҢзңҹиҝҷд№ҲеҘҪпјҹдёәжӯӨпјҢжҲ‘们еҒҡдәҶ2000е…¬йҮҢзҡ„й•ҝжөӢ
- жңүи°ҒзҹҘйҒ“е…ідәҺ еҺӮеӯҗйҮҢзҡ„дёҖдәӣдҝЎжҒҜ жҲ–д»Ӣз»ҚдёҖдәӣеҸӘжңүиҝӣдәҶеҺӮеӯҗжүҚиғҪзҹҘйҒ“зҡ„з»ҸеҺҶ
- е…ідәҺеӣҫзүҮйҮҢзҡ„ж–Үжң¬иҜҶеҲ«пјҢе“Әдәӣзү№еҫҒзӣёеҜ№жңүж•Ҳ










![[з»“еҜ№]дёӯеӨ©йҮ‘иһҚз»“еҜ№её®жү¶еӣўз»“жқ‘дёүе№ҙй—ҙпјҡиҠұејҖеңЁзңјеүҚ](https://p0.ssl.qhimgs4.com/t01b6de3abbdb96b907.jpg)
![[жҲҙе®үеЁңзҺӢеҰғ]еЁҒе»үзҺӢеӯҗзңҹжҹ”жғ…пјҒжң¬жқҘејҖеҝғзәӘеҝөжҲҙе®үеЁңеҝҪ然жіӘжөҒдёҚжӯўпјҢеҮҜзү№дёҚзҹҘжүҖжҺӘ](http://img88.010lm.com/img.php?https://image.uc.cn/s/wemedia/s/upload/2020/7754129187927f96deeb591e11f75cdd.jpg)