еҰӮдҪ•зі»з»ҹең°ж¬әйӘ—еӣҫеғҸиҜҶеҲ«зҘһз»ҸзҪ‘з»ң( дәҢ )
еӣ дёә ? жҳҜвҖңдёҚеҸҜжЈҖжөӢвҖқзҡ„пјҲжҲ–иҖ…еҮ д№ҺдёҚеҸҜжЈҖжөӢпјү пјҢ жүҖд»Ҙе®ғеңЁи§Ҷи§үдёҠеҜ№еӣҫеғҸеә”иҜҘжІЎжңүд»Җд№ҲдёҚеҗҢ гҖӮ дҪҶжҳҜ пјҢ жҜҸдёҖдёӘеҸҳеҢ–йғҪжҳҜжҢүз…§ sign еҮҪж•°жһ„е»әзҡ„ пјҢ иҝҷж ·еҠ жқғе’Ңзҡ„еҸҳеҢ–жҳҜжңҖеӨ§зҡ„ гҖӮ
еӣ жӯӨ пјҢ жҲ‘们е°Ҷ -? жҲ– +? ж·»еҠ еҲ°иҫ“е…Ҙеҗ‘йҮҸзҡ„жҜҸдёӘе…ғзҙ дёҠ пјҢ иҝҷжҳҜдёҖдёӘи¶іеӨҹе°Ҹзҡ„еҸҳеҢ– пјҢ д»ҘиҮідәҺе®ғдёҚеҸҜжЈҖжөӢ пјҢ дҪҶдҪҝз”Ё sign еҮҪж•°жһ„йҖ пјҢ д»ҺиҖҢдҪҝеҸҳеҢ–жңҖеӨ§еҢ– гҖӮ
и®ёеӨҡе°Ҹ组件еҠ иө·жқҘеҸҜиғҪдјҡеҸҳеҫ—йқһеёёеӨ§ пјҢ зү№еҲ«жҳҜеҰӮжһңе®ғ们жҳҜдёҖз§ҚжҷәиғҪзҡ„ж–№ејҸжһ„йҖ зҡ„иҜқ гҖӮ
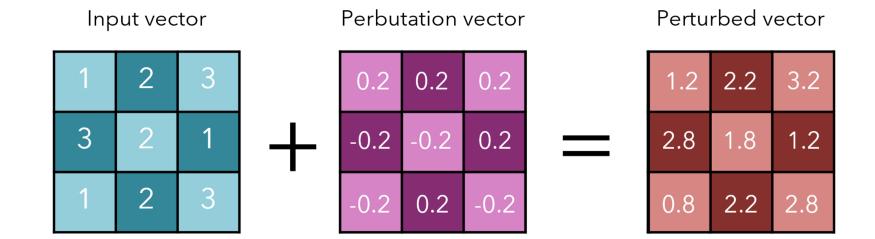
и®©жҲ‘们иҖғиҷ‘дёҖдёӢеңЁдёҠдёҖдёӘдҫӢеӯҗдёӯ ?=0.2 ж—¶иҝҷз§Қжғ…еҶөзҡ„еҪұе“Қ гҖӮ жҲ‘们еҸҜд»Ҙеҫ—еҲ° 3 дёӘеҚ•дҪҚзҡ„е·®йўқпјҲжҖ»е’Ңдёә -4пјү гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
иҝҷжҳҜзӣёеҪ“еҸҜи§Ӯзҡ„ пјҢ зү№еҲ«жҳҜиҖғиҷ‘еҲ° perbutation еҗ‘йҮҸеҜ№еҺҹе§Ӣиҫ“е…Ҙеҗ‘йҮҸзҡ„еҫ®е°ҸеҸҳеҢ– гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
и®©жҲ‘们иҖғиҷ‘дёҖдёӢеңЁдёҠдёҖдёӘдҫӢеӯҗдёӯ ?=0.2 ж—¶иҝҷз§Қжғ…еҶөзҡ„еҪұе“Қ гҖӮ жҲ‘们еҸҜд»Ҙеҫ—еҲ° 3 дёӘеҚ•дҪҚзҡ„е·®йўқпјҲжҖ»е’Ңдёә -4пјү гҖӮ
еҰӮжһңжқғйҮҚеҗ‘йҮҸе…·жңү n дёӘз»ҙж•° пјҢ 并且е…ғзҙ зҡ„е№іеқҮз»қеҜ№еҖјдёә m пјҢ еҲҷжҝҖжҙ»еҖје°Ҷеўһй•ҝдёә ?nm гҖӮ еңЁй«ҳз»ҙеӣҫеғҸдёӯпјҲеҰӮ 256Г—256Г—3пјү пјҢ n зҡ„еҖјдёә 196608 гҖӮ m е’Ң ? еҸҜд»Ҙйқһеёёе°Ҹ пјҢ дҪҶд»ҚдјҡеҜ№иҫ“еҮәдә§з”ҹйҮҚеӨ§еҪұе“Қ гҖӮ
иҝҷз§Қж–№жі•йқһеёёеҝ« пјҢ еӣ дёәе®ғеҸӘйҖҡиҝҮ +? жҲ– -? жқҘж”№еҸҳиҫ“е…ҘпјҡдҪҶжҳҜе®ғиҝҷж ·еҒҡзҡ„ж–№ејҸеҰӮжӯӨжңүж•Ҳ пјҢ д»ҘиҮідәҺе®Ңе…Ёж„ҡеј„дәҶзҘһз»ҸзҪ‘з»ң гҖӮ
 ж–Үз« жҸ’еӣҫ
ж–Үз« жҸ’еӣҫ
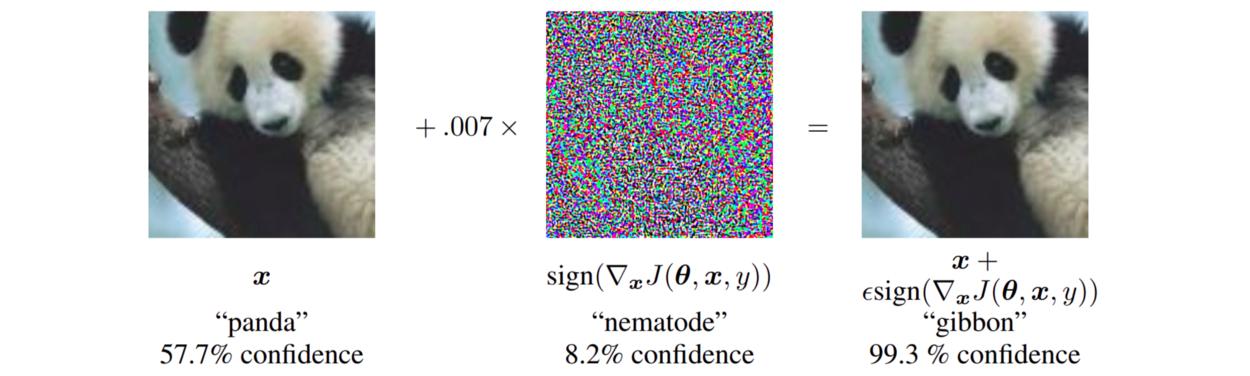
еңЁдёҠеӣҫдёӯ пјҢ 0.007 зҡ„ ? еҜ№еә”дәҺ GoogLeNet иҪ¬жҚўдёәе®һж•°д№ӢеҗҺзҡ„ 8 дҪҚеӣҫеғҸзј–з Ғзҡ„жңҖе°Ҹдёәзҡ„еӨ§е°Ҹ гҖӮ жқҘжәҗпјҡ Goodfellow зӯүдәә гҖӮ
Goodfellow зӯүдәәеңЁеә”з”Ё FGSM ж—¶еҸ‘зҺ°дәҶжңүи¶Јзҡ„з»“жһңпјҡ
- ?=0.25 ж—¶ пјҢ жө…еұӮ SoftMax еҲҶзұ»еҷЁзҡ„й”ҷиҜҜзҺҮдёә 99.9% пјҢ MNIST дёҠзҡ„е№іеқҮзҪ®дҝЎеәҰдёә 79.3% гҖӮ
- ?=0.1 ж—¶ пјҢ еҜ№йў„еӨ„зҗҶзҡ„ CIFAR-10 зҡ„й”ҷиҜҜйў„жөӢ пјҢ CNN зҡ„й”ҷиҜҜзҺҮдёә 87.15% пјҢ е№іеқҮзҪ®дҝЎеәҰдёә 96.6% гҖӮ
иҝҷдәӣеҜ№жҠ—жҖ§зҡ„иҫ“е…Ҙ / ж ·жң¬еҸҜд»Ҙи§ЈйҮҠдёәй«ҳз»ҙзӮ№з§Ҝзҡ„дёҖдёӘзү№жҖ§пјҡеҪ“йңҖиҰҒеңЁе…¶дёӯеҲҶй…Қе’Ңзҡ„еғҸзҙ ж•°йҮҸиҫғеӨҡж—¶ пјҢ еҠ жқғе’ҢеҸҜд»ҘжӣҙеӨ§ пјҢ иҖҢеҜ№жҜҸдёӘеҚ•зӢ¬еғҸзҙ зҡ„ж”№еҸҳд№ҹдјҡжӣҙе°Ҹ гҖӮ
дәӢе®һдёҠ пјҢ еҜ№жҠ—жҖ§ж ·жң¬жҳҜзҪ‘з»ңиҝҮдәҺзәҝжҖ§зҡ„з»“жһң гҖӮ жҜ•з«ҹ пјҢ иҝҷж ·зҡ„еҸҳеҢ–пјҲжҜ”еҰӮиҜҙпјүеҜ№дёҖдёӘз”ұ sigmoid еҮҪж•°з»„жҲҗзҡ„зҪ‘з»ңзҡ„еҪұе“Қеҫ®д№Һе…¶еҫ® пјҢ еӣ дёәеңЁеӨ§еӨҡж•°ең°ж–№ пјҢ perbutation зҡ„еҪұе“ҚйғҪжҳҜйҖ’еҮҸзҡ„ гҖӮ е…·жңүи®ҪеҲәж„Ҹе‘ізҡ„жҳҜ пјҢ жӯЈжҳҜиҝҷз§Қзү№жҖ§вҖ”вҖ”жӯ»дәЎжўҜеәҰпјҲdying gradientsпјүReLU е’Ңе…¶д»–е®№жҳ“еҸ—еҲ°еҜ№жҠ—жҖ§иҫ“е…ҘеҪұе“Қзҡ„ж— з•ҢеҮҪж•°зҡ„е…ҙиө· гҖӮ
жң¬ж–ҮдёӯжҸҗеҮәзҡ„е…¶д»–иҰҒзӮ№еҢ…жӢ¬пјҡ
- жңҖйҮҚиҰҒзҡ„жҳҜ perbutation зҡ„ж–№еҗ‘ пјҢ иҖҢдёҚжҳҜз©әй—ҙдёӯзҡ„жҹҗдёӘзү№е®ҡзӮ№ гҖӮ иҝҷ并дёҚжҳҜиҜҙ пјҢ жЁЎеһӢеңЁеӨҡз»ҙз©әй—ҙдёӯеӯҳеңЁвҖңејұзӮ№вҖқзҡ„жғ…еҶөпјӣзӣёеҸҚ пјҢ еңЁеҜ№жҠ—жҖ§иҫ“е…Ҙзҡ„жһ„е»әдёӯ пјҢ perbutation зҡ„ж–№еҗ‘жүҚжҳҜжңҖе…ій”®зҡ„ гҖӮ
- еӣ дёәж–№еҗ‘жҳҜжңҖйҮҚиҰҒзҡ„ пјҢ жүҖд»ҘеҜ№жҠ—жҖ§з»“жһ„еҸҜд»ҘжіӣеҢ– гҖӮ з”ұдәҺеҜ»жүҫеҜ№жҠ—жҖ§иҫ“е…Ҙ并дёҚеұҖйҷҗдәҺжҺўзҙўжЁЎеһӢзҡ„йў„жөӢз©әй—ҙ пјҢ еӣ жӯӨ пјҢ еҸҜд»ҘеңЁйӣҶдёӯдёҚеҗҢзұ»еһӢе’Ңз»“жһ„зҡ„жЁЎеһӢдёҠжҺЁе№ҝжһ„йҖ ж–№жі• гҖӮ
- еҜ№жҠ—жҖ§и®ӯз»ғеҸҜд»ҘеҜјиҮҙжӯЈеҲҷеҢ– пјҢ з”ҡиҮіжҜ” Dropout иҝҳиҰҒеӨҡ гҖӮ и®ӯз»ғзҪ‘з»ңиҜҶеҲ«еҜ№жҠ—жҖ§иҫ“е…ҘжҳҜдёҖз§Қжңүж•Ҳзҡ„жӯЈеҲҷеҢ–еҪўејҸ пјҢ д№ҹи®ёжҜ” Dropout жӣҙжңүж•Ҳ гҖӮ еҜ№жҠ—жҖ§и®ӯз»ғзҡ„жӯЈеҲҷеҢ–ж•ҲжһңдёҚиғҪйҖҡиҝҮеҮҸе°‘жқғйҮҚжҲ–з®ҖеҚ•ең°еўһеҠ жқғйҮҚжқҘеӨҚеҲ¶ гҖӮ
- жҳ“дәҺдјҳеҢ–зҡ„жЁЎеһӢеҫҲе®№жҳ“еҸ—еҲ°жү°еҠЁ гҖӮ еҰӮжһңжүҫеҲ°жңҖдҪіжўҜеәҰеҫҲз®ҖеҚ• пјҢ йӮЈд№Ҳи®Ўз®—дёҖдёӘжңүж•Ҳзҡ„еҜ№жҠ—жҖ§иҫ“е…ҘеҗҢж ·д№ҹдјҡеҫҲз®ҖеҚ• гҖӮ
- зәҝжҖ§жЁЎеһӢгҖҒи®ӯз»ғд»ҘжЁЎжӢҹиҫ“е…ҘеҲҶеёғзҡ„жЁЎеһӢд»ҘеҸҠйӣҶеҗҲеҜ№жҠ—жҖ§иҫ“е…ҘеқҮдёҚиғҪжҠөжҠ—еҜ№жҠ—жҖ§иҫ“е…Ҙ гҖӮ RBF зҪ‘з»ңе…·жңүжҠөжҠ—жҖ§ гҖӮ е…·жңүйҡҗи—ҸеұӮзҡ„жһ¶жһ„еҸҜд»ҘйҖҡиҝҮи®ӯз»ғжқҘиҜҶеҲ«еҜ№жҠ—жҖ§иҫ“е…Ҙ пјҢ д»ҺиҖҢиҺ·еҫ—дёҚеҗҢзЁӢеәҰзҡ„жҲҗеҠҹ гҖӮ
жҺЁиҚҗйҳ…иҜ»
- и°·жӯҢе»әз«Ӣж–°AIзі»з»ҹ еҸҜејҖеҸ‘з”ңе“Ғй…Қж–№
- еӨ§дёҖйқһи®Ўз®—жңәдё“дёҡзҡ„еӯҰз”ҹпјҢеҰӮдҪ•еҲ©з”ЁеҜ’еҒҮиҮӘеӯҰCиҜӯиЁҖ
- иҜәеҹәдәҡдёәдҪ•е®ҒеҸҜйҖҗжёҗжІЎиҗҪд№ҹдёҚйҮҮз”ЁAndroidзі»з»ҹпјҹй•ҝзҹҘиҜҶдәҶ
- зғҹеҸ°жёҜвҖңз®ЎйҒ“жҷәи„‘зі»з»ҹвҖқдёҠзәҝ еңЁеӣҪеҶ…зҺҮе…Ҳе®һзҺ°еҺҹжІ№еӮЁиҝҗе…ЁжҒҜжҷәиғҪжҺ’дә§
- vivoдёҖж¬ҫж–°жңәзҺ°иә«и·‘еҲҶзҪ‘пјҒиҝҗеӯҳе’Ңзі»з»ҹдҝЎжҒҜйҖҡйҖҡжӣқе…ү
- зәўзұіK40жёІжҹ“еӣҫжӣқе…үпјҡеұ…дёӯжҢ–еӯ”+еҗҺзҪ®еӣӣж‘„пјҢиҝҷеӨ–и§ӮдҪ и§үеҫ—еҰӮдҪ•пјҹ
- еҘӢж–—|иҜҘеҰӮдҪ•зңӢеҫ…жӢјеӨҡеӨҡе‘ҳе·ҘзҢқжӯ»пјҡйј“еҠұеҘӢж–—пјҢд№ҹиҰҒдҝқжҠӨеҘҪеҘӢж–—иҖ…
- дәәз‘һдәәжүҚ(06919)пјҡжңӘжқҘ3е№ҙзі»з»ҹе№іеҸ°е°ҶеҸ‘еҠӣжҷәиғҪеҢ–пјҢжү“йҖ иҒҢдёҡз”ҹжҖҒй“ҫе№іеҸ°
- иЈ…жңәзӮ№дёҚдә® еҰӮдҪ•з®Җжҳ“жҺ’жҹҘ硬件问йўҳпјҹ
- ж¶Ҳиҙ№иҖ…жҠҘе‘Ҡ | зҫҺеӣўе……з”өе®қз”өйҮҸдёҚи¶ід№ҹжүЈиҙ№пјҢжҳҜиҙЁйҮҸй—®йўҳиҝҳжҳҜзі»з»ҹзјәйҷ·пјҹ
















