凝聚态|对称破缺——凝聚态中的物理美( 二 )
传统的科研方法以还原论为主 , 古希腊的科学就是从“追本溯源” , 即“还原”开始的 。 所谓还原论 , 就是认为复杂系统可以化解为各部分的组合 , 并且 , 复杂体系的行为可以用其部分的行为来加以理解和描述 。 例如 , 物质由分子组成 , 分子由原子组成 , 原子又由更深一层的基本粒子组成 , 依次递推 , 构成了物质结构中越来越小的层次 。 还原论的方法便是逐层级地回答问题 , 期待深一层的结构能解释上一个层次所表现的性质 。 如此下去 , 科学演化的路线似乎归结为一条还原的路线 , 最后追溯到一个“终极问题” 。
然而 , 安德森提出不同的观点 。 他认为“多则异” , 还原并不能重构宇宙 , 部分行为不能完全解释整体行为 。 高层次物质的规律不一定是低层次规律的应用 , 并不是只有底层基本规律是基本的 , 每个层次皆要求全新的基本概念的构架 , 都有那一个层次的基础原理 。 也就是说 , 安德森教给我们不同于还原论的另一种认识这个世界的视角 , 即“层展论”(或称整体论)的观点 。 层展论既不属于还原论 , 也不反对还原论 , 而是与还原论互补 , 构成更为完整的科学方法 。
安德森在他的《多则异》的文章中 , 以凝聚态中的对称破缺为例 , 说明层展论 。
相变——对称和对称破缺
对称性的概念不难理解 , 在自然界及人工的建筑、艺术等领域 , 几何对称现象随处可见 。 固体中的晶格是一种空间状态重复的几何对称结构 。 如果将整个晶体移动一个晶格常数a , 结果仍然是原来的系统 。 换言之 , 晶格结构具有在空间平移a的变换下系统保持不变的对称性 。 所以 , 对称的意思就是系统在某种变换下保持状态不变 。 除了空间平移变换之外 , 还有空间旋转、空间反演等等其它种类的变换 。 除了在三维空间的各种变换之外 , 还有对于时间的平移或反演变换 , 以及其它抽象的或内禀性质的变换 。 各种变换对应于各种不同的对称性 。
物理学中有一个诺特定理(Noether's theorem) , 由德国女数学家埃米·诺特(Emmy Noether , 1882-1935)发现 , 它将物理中的守恒定律与对称性联系在一起[5] 。 例如 , 能量守恒定律对应时间对称性;动量守恒对应空间平移对称;角动量守恒对应旋转对称性等等 。 我们在此不予详述 , 可见参考资料[6] 。
大千世界不仅有对称 , 也有不对称 。 观察我们周围的世界:人的左脸并不完全等同于右脸 , 大多数人的心脏长在左边 , 大多数的DNA分子是右旋的 , 地球并不是一个完全规则的球形……正是因为对称中有了这些不对称的元素 , 对称与不对称的和谐交汇 , 才创造了我们丰富多彩的世界 。
即便是对称的情况 , 也有各种等级的高低之分 。 比如说 , 一个正三角形 , 和一个等腰三角形比较 , 正三角形应该更为对称一些;球面比椭球面具有更多的对称性 。 此外 , 物体状态的对称性也会变化 , 从低到高 , 或者从高到低 。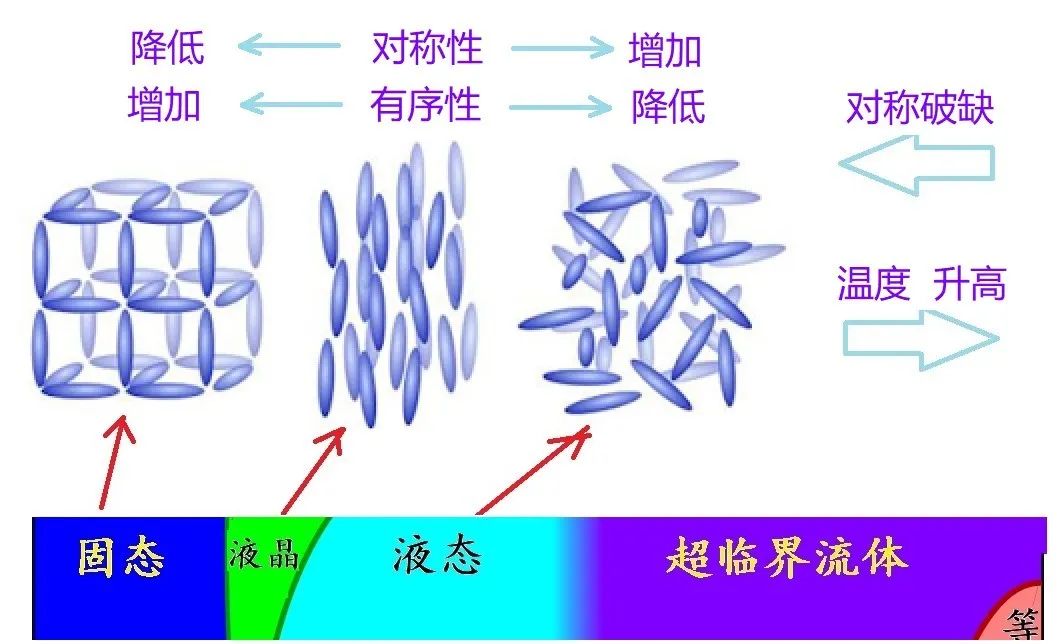
图4:相变和对称破缺
朗道将凝聚态物理中的相变与物质结构中对称性的变化联系在一起 。 他把从高对称到低的对称过程叫做“对称破缺” 。 相应的 , 反过来的相变则意味着“对称恢复” 。 然而 , 如何判断对称性的“高低”呢?特别需要提醒的是:有时候我们会将“对称性”与“有序性”等同起来 , 但事实上这两个概念的“高低”程度正好相反 。 越有序的结构 , 对称性反而越低 。 以下举个简单例子来说明 。
图4上方所示的是“固态→液晶→液态”过程中物质分子结构的变化 。 这三者的对称性 , 到底孰高孰低呢?
固态中水分子有次序地排列起来 , 形成整齐漂亮的格子或图案(晶格);在液晶中 , 三维晶格被破环了 , 成为一维晶体 。 之后 , 随着温度继续升高 , 一维的有序结构也被破坏而成为无序的液体:液态中的水分子做着随机而无规则的布朗运动(Brownian Motion)——没有固定的方向 , 没有固定的位置 , 处于完全无序的状态 , 在任何方向、任何点看起来都是一样的 。 而这正是我们所谓的对称性最“高”的状态 , 也就是说 , 液态的对称性很高 , 却无序 。 液晶和固态 , 相较液态而言 , 有序程度逐渐增加 , 对称性却逐步降低 。
用数学的语言来描述的话 , 液态时 , 如果将空间坐标作任何平移变换 , 系统的性质都不会改变 , 表明对空间的高度对称 。 而当水结成冰之后 , 系统只在沿着某些空间方向 , 平移晶格常数a的整数倍的时候 , 才能保持不变 。 所以 , 物质从液态到固态 , 对称性降低 , 也就是破缺了 , 从连续的平移对称性减少成了离散的平移对称性 。 或叫做:固态破缺了液态的连续平移对称性 , 即晶体是液体的任意平移对称性破缺的产物 。 相比于液体 , 晶体的粒子密度出现了空间上的周期调制 , 因而更加有序 , 而从无到有的周期调制的变化 , 便可以表征物质从液体结晶为固体时的相变 。
对称破缺(Symmetry Breaking)分为两大类:明显对称性破缺(Explicit Symmetry Breaking)和自发对称性破缺(Spontaneous Symmetry Breaking) 。 第一类“对称破缺”的原因是自然规律决定的 , 是因为某些物理系统本身就不具有某些物理规律对应的对称性 , 这类对称破缺的著名例子是李政道与杨振宁发现的“弱相互作用中宇称不守恒”(CP violation) 。
推荐阅读
- 朔城区新联会|朔城区新联会:肩负使命担当 凝聚奋进力量 践行报国理想
- 不对称战争|1元更香!阿里打响不对称战争,名创优品开始焦虑
- 每日谈资|《青暂行》面临“糊剧”危机!对称海报再惹祸端,杨紫吴亦凡粉丝水火不容
- 东钱湖|凝聚智慧 启迪未来——首届“东钱湖教育论坛”开幕
- 诊疗|支修益:凝聚前沿创新力量,将肺癌教育深化落地
- 家长|凝聚家校育人合力 这所学校点子多
- 蚂蚁|蚂蚁集团与杭州市政府战略合作:为杭州凝聚全球金融科技生态