数学|分享小学经典图形题,能做对者成绩不会差,解题关键是等积代换
各位朋友 , 大家好!今天是2020年8月29日星期六 , 数学世界将继续为大家分享小学各年级的数学竞赛题 , 今天我们仍然讲解一道有关求阴影部分的面积的图形题 , 此内容涉及小学数学中的三角形和梯形面积的知识 , 属于思维拓展类型 。 数学世界希望对题目的分析与讲解能够给大家的学习一些帮助!
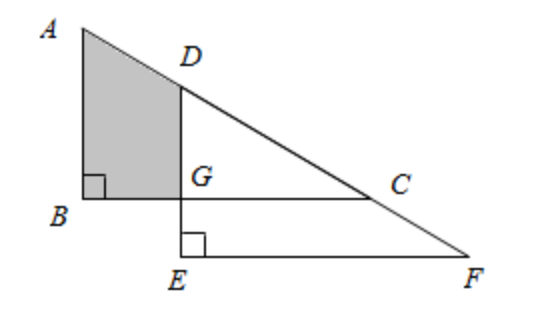
例题:(小学数学竞赛题)如图所示 , 将图中的直角三角形ABC向右平移4厘米 , 再向下平移1.5厘米 , 刚好到三角形DEF的位置 , 已知EF=10cm , 求阴影部分的面积是多少平方厘米?
这是一道比较新颖的题目 , 所要求的阴影部分是一个规则图形 , 可以通过常见面积公式直接来求 , 但是对于求梯形的面积 , 还有一些未知条件 , 并且无法求出来 , 很多学生对此可能毫无办法 。 接下来 , 数学世界就与大家一起来完成这道例题吧!
分析:根据图形 , 我们可以看出:直角三角形向右平移4厘米 , 即BG=4厘米 , 再向下平移1.5厘米 , 即EG=1.5厘米 。 已知EF=10cm , 则GC=10-4=6厘米 。 由于两个三角形都是同一个三角形平移得到 , 当这两个三角形都去掉公共部分(即三角形DCG) , 则剩余部分的面积仍然相等 。
于是得到:阴影部分的面积=梯形GEFC的面积 , 先求出梯形GEFC的上底和高 , 进而利用梯形的面积公式:S=(a+b)h÷2即可求解 , 于是问题得到解决 。 下面 , 我们就按照以上思路解答此题吧!
解答:因为直角三角形ABC向右平移4厘米 ,
所以BG=4厘米 ,
因为直角三角形ABC向下平移1.5厘米 ,
所以EG=1.5厘米 ,
因为直角三角形ABC和三角形DCG面积相等 ,
所以阴影部分的面积=梯形GEFC的面积 ,
因为梯形GEFC的上底GC=10-4=6厘米 ,
高EG=1.5厘米 , 下底EF=10厘米 ,
所以梯形GEFC的面积为:
1/4×3.14×40=31.4(平方厘米)
则阴影部分的面积为:
(10+6)×1.5÷2
=16×1.5÷2
=12(平方厘米)
【数学|分享小学经典图形题,能做对者成绩不会差,解题关键是等积代换】答:阴影部分的面积是12平方厘米 。
(完毕)
这道题主要考查了梯形面积公式的运用 , 解答此题的关键是弄清楚:阴影部分的面积=梯形GEFC的面积 。 温馨提示:朋友们如果有不明白之处或者有更好的解题方法 , 欢迎大家在下面留言讨论 。 谢谢!
推荐阅读
- 数学|你见过最讽刺的事是什么?信心满满把试卷给我抄成倒数第二!
- 数学|事业单位又涨工资?除了它,这行也成“香饽饽”,工资不输公务员
- 数学|我们一个被“嫌弃”了23年的数学天才,累死才知道他的价值
- 钱钟书|他高考数学仅有15分,校长复查试卷后十分激动,道:就他了
- 教师节|教师节前,一家长举报自己孩子的小学班主任收受礼金,老师被开除
- 中小学|一年级99分语文试卷火了,卷面让老师不舍扣分,自律的孩子真棒
- 数学|我国“最难考”的10所理工大学,录取分超600分,学霸:不在话下
- 中小学|“高中班主任成了我的老公?!”那些年做过的轰动全校的事
- 数学|数学题:一个四位数与它的各个位上的数之和是1972,求这个四位数
- 中小学|初中时同学家里几个亿,班里的班费被偷了,老师们冤枉他偷班费!