超导体|80年前的马约拉纳猜想,和当今火爆的拓扑量子计算有什么关系?
出品:"格致论道讲坛"公众号(ID:SELFtalks)
以下内容为上海交通大学贾金锋演讲实录:
大家好 , 我的名字叫贾金锋 , 我今天做的报告题目是“寻找马约拉纳费米子” 。
看到这个题目 , 大家可能有一大堆问题 。 首先 , 什么是马约拉纳费米子?
【超导体|80年前的马约拉纳猜想,和当今火爆的拓扑量子计算有什么关系?】基本粒子
要了解马约拉纳费米子 , 首先我们要知道什么是费米子 。
大家熟知的粒子是原子、分子 。 物质世界就是由这些原子、分子组成的 , 它们是保持物质性质最小的基本单元 。
如果把原子、分子再往下分 , 就会分出很多被叫做“基本粒子”的东西 , 比如夸克、轻子、胶子、光子等 。 它们比原子分子更小 , 是组成物质世界的单元 , 我们叫做基本粒子 。
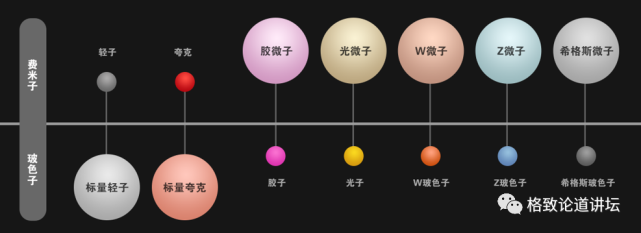
这么多的基本粒子要怎么研究呢?
一位天才的科学家叫做狄拉克 , 他把基本粒子分成两类 , 一类叫费米子 , 一类叫玻色子 。
玻色和费米 , 他们两位都是非常伟大的科学家 。 为了纪念他们 , 所以狄拉克用他们的名字命名了这两类基本粒子 。
狄拉克还预言 , 每一种基本粒子都存在一种反粒子 。 比如说 , 电子是一种费米子 , 我们用的电就是由电子产生的 , 它的反粒子就是正电子 。
所以 , 到目前我们知道了什么是费米子 , 什么是玻色子 , 每种粒子会有反粒子 。
在这之后 , 出现了一位更伟大的科学家 , 他叫马约拉纳 , 这是一位非常天才的科学家 。

这个天才不是我说的 , 是跟他一起工作的费米说的 , 费米就是刚才费米子的费米 。 费米本身就是一个非常天才的科学家 , 他很少夸别人是天才 , 但是他夸马约拉纳是一个天才 , 可想而知马约拉纳是多么天才了 。
马约拉纳做了这么一个预想:在狄拉克方程的基础上 , 他预想存在一种神奇的粒子 , 它和它的反粒子一模一样 , 即正反粒子都是它自身 , 这个预想中的粒子被称为马约拉纳费米子 。
现在大家清楚什么是马约拉纳费米子了吧 。 首先要知道清楚什么是费米子 , 然后费米子都有反粒子 , 如果反粒子和自己一样 , 那就是马约拉纳费米子 。
为什么要找马约拉纳费米子?马约拉纳费米子有什么好的地方?
一方面 , 从理论上来讲 , 马约拉纳做了这样一个预言 , 不仅因为他是一个天才的科学家 , 而且这个预言本身就意义非凡 。 如果你找到了马约拉纳费米子 , 就证明了马约拉纳理论的正确性 , 这对科学研究来说非常重要 。
另一方面 , 证明马约拉纳费米子的存在 , 有利于理解其他学科理论 。 比如 , 我们常听说的一个暗物质 , 暗物质理论提出以后 , 有科学家预言 , 暗物质的备选粒子也是马约拉纳费米子 。 所以 , 如果我们能够找到马约拉纳费米子 , 将有助于人们理解暗物质 。
更重要的是 , 马约拉纳费米子还可以做拓扑量子计算 。
所以 , 马约拉纳费米子除了在理论上、基础研究上有重要性之外 , 还可以用来做拓扑计算 。
马约拉纳费米子既有非常重要的理论意义 , 在实际应用中也很重要 , 所以马约拉纳的预言出来之后 , 人们一直在找寻它 。
怎么找到马约拉纳费米子呢?
怎么找?下面我就讲讲我们是怎么找马约拉纳费米子的 。
实际上 , 我们找的马约拉纳费米子是一种准粒子 , 不是像电子、质子这样的真粒子 。
准粒子是个什么概念呢?就是性质像粒子 , 但本质并不是粒子 。
在凝聚态物理体系里 , 如果你把很多个电子、原子按照某种形式组合起来 , 这个整体可以表现出与马约拉纳费米子同样的性质 , 同样遵从马约拉纳方程 , 我们就把这种组合叫做“准”马约拉纳费米子 。
所以 , 我们要找的并不是一个真的单个粒子 , 而是在固体里面表现出马约拉纳费米子特性的多个电子、原子的组合 , 被称为“准”马约拉纳费米子的东西 。
知道这个以后 , 我们就可以开始进行下一步了 , 看看怎么找这个马约拉纳费米子 。
有科学家提出 , 马约拉纳费米子存在于一种叫做拓扑超导的材料里面 。
所有自然界的材料 , 它们有导电的 , 有不导电的 , 导电的叫导体 , 不导电的叫绝缘体 , 电阻值为零的导体叫超导体 。
后来人们发现了一种内部绝缘但表面导电的特殊绝缘体 , 叫做拓扑绝缘体 。 拓扑什么意思呢?就是指这种材料的“表面”在一种保护下能够保持其导电性质“不变” 。
那有没有可能存在一种跟拓扑绝缘体相对应的拓扑超导体呢?
实际上 , 我们在自然界中发现了成千上万种超导体 , 没有一种是拓扑超导体 。
拓扑超导体在自然界中是不存在的 , 这就是一个很大的问题 。
有一个理论预言 , 如果把拓扑绝缘体和超导体放在一起 , 通过一种巧妙的方式组合起来 , 就可以组合成拓扑超导体 。
一旦组合出这种拓扑超导体 , 就可以帮助我们寻找马约拉纳费米子了 。
但是 , 组合拓扑超导体并不是那么容易 , 我们在做这个实验之前 , 有一定的实验积累 。
我们把扫描隧道显微镜和一种叫“分子束外延”的寻找材料方法结合起来 , 一个原子层一个原子层地去找原子 , 这样找出来的材料 , 应该是世界上最好的纯度 。
有了这些技术以后 , 经过多次反复试验 , 我们找出了拓扑超导体 , 并且通过巧妙的设计 , 把这个拓扑超导体设计成比较有利于实验观察的形式 。
我们实验中使用的扫描隧道显微镜 , 是目前唯一能够在实空间里看见真实原子的显微镜 , 它的放大倍数非常大 。
说起来这个显微镜很神奇 , 但是它的原理很简单 。
在扫描隧道显微镜中 , 有一根非常尖的针 , 我们用它去“摸”材料表面 , 如果原子有起伏 , 显微镜就能“感觉”出来 。 这就好比我们用手指头在物体表面触摸就能感受它表面的起伏一样 。

针从表面上划过的时候 , 我们去测量针和原子之间的电流 。 如果针和原子之间非常近 , 电流就很大 , 远 , 电流就小 , 这样我们就可以通过观察电流的大小来判断有没有原子 。
另外 , 我们用的这个针有磁性 。 因此 , 表面上有磁性的原子和没磁性的原子就可以区别开来 。
这样 , 我们用扫描隧道显微镜 , 既可以研究表面上的结构 , 也可以研究表面上的磁性 , 对寻找马约拉纳费米子非常有利 。

这个显微镜就是自旋极化扫描隧道显微镜 。 在此基础上 , 就可以开始关于马约拉纳费米子的研究了 。
其实 , 我们的研究也不是那么容易 , 找到了拓扑超导材料 , 又有了高级的设备 , 我们还是花费了好几年的时间来寻找马约拉纳费米子 , 为什么?
原因就是我们并不知道马约拉纳费米子到底长什么模样 , 它和普通的超导体有什么区别 。 究竟看见什么样的东西才能确定它是真正的马约拉纳费米子?
摸索了好几年以后 , 我们终于找到了一种叫做自旋极化电流的东西 。
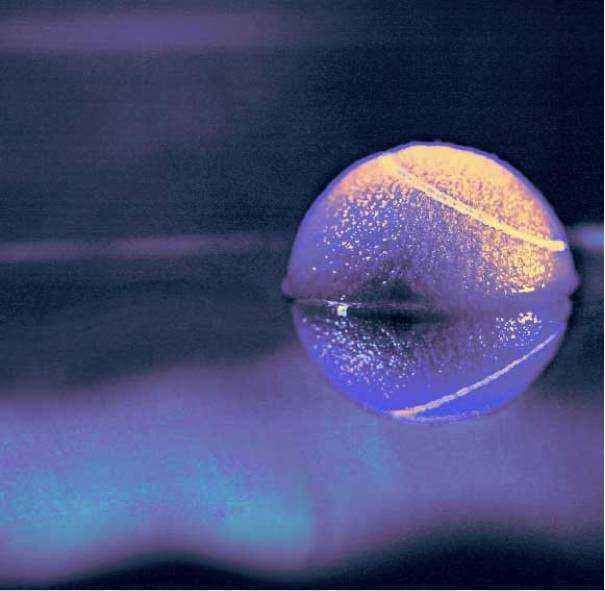
这就是我们用的拓扑超导样品 , 其实样品很小 , 真正起作用的就是中间一小点 。 我们在拓扑超导样品上观察到了自旋极化电流确实是由马约拉纳费米子产生的 。

通过这个观察 , 我们证明了马约拉纳费米子的存在 。
马约拉纳费米子与拓扑量子计算
最后我们再来讲一下 , 马约拉纳费米子的发现对我们有什么用?
我刚才讲了 , 它可以用来做拓扑量子计算 。
量子计算非常有用 , 计算速度非常快 , 其计算能力超过了目前全世界计算能力的总和 。
但是 , 量子计算并不是那么容易实现的 , 原因之一就是你想把所有的量子比特纠缠起来并保持一个相当长的时间 , 再在这段时间之内来完成量子计算 , 是很困难的 , 其中有很多噪音、杂质的影响 。 所以到2016年为止 , 量子计算还没有实现 。
为了克服外界因素的干扰 , 人们就提出了另外一个实现量子计算的方法 , 就是拓扑量子计算 。
拓扑量子计算就是利用拓扑性质 , 来保护量子比特不受干扰 , 解决纠错等问题 , 从而使实现量子计算更加容易
但是拓扑量子计算完全是一个假想出来的方案 , 这个方案需要结合任意子 。 任意子是一种更奇特的东西 , 它是一种臆想出来的粒子 。
但只有有了任意子 , 我们才能做拓扑量子计算 。
可喜的是 , 我们找到的马约拉纳费米子恰恰就是一种任意子 , 这就是马约拉纳费米子能用于拓扑量子计算的原因 。 所以它是实现拓扑量子计算的一种很好的材料 。
我们希望接着往下研究 , 能够在近期把马约拉纳费米子弄清楚 , 用它来做拓扑量子计算 。
其实 , “马约拉纳费米子能在凝聚态体系中实现”的想法被提出来 , 很多国家已经开始布局了 。 在马约拉纳费米子的研究以及拓扑量子计算的研究方面 , 欧美已经投入了大量资金 。
微软从2010年开始投资这个方向 , 五年为一个周期 , 现在进入到第二个周期 。 目前拓扑量子计算方法、马约拉纳费米子的研究进展非常快 , 国际上几十个团队都在研究这个领域 。
我们能够率先找到马约拉纳费米子是非常幸运的一件事 , 我们希望能够在国家的支持下 , 接着往前走 , 希望在五年到十年之内 , 我们能找出用马约拉纳费米子做的量子比特 , 然后进一步实现拓扑量子计算 。
通过我的演讲 , 希望大家能够明白 , 什么是马约拉纳费米子 , 马约拉纳费米子有多么重要 , 找到马约拉纳费米子以后对我们将来的生活有什么样的影响 , 谢谢大家 。
【超导体|80年前的马约拉纳猜想,和当今火爆的拓扑量子计算有什么关系?】“格致论道” , 原称“SELF格致论道” , 是中国科学院全力推出的科学文化讲坛 , 由中国科学院计算机网络信息中心和中国科学院科学传播局联合主办 , 中国科普博览承办 。 致力于非凡思想的跨界传播 , 旨在以“格物致知”的精神探讨科技、教育、生活、未来的发展 。 获取更多信息 。 本文出品自“格致论道讲坛”公众号(SELFtalks) , 转载请注明公众号出处 , 未经授权不得转载 。
推荐阅读
- 养老金|2021年上半年办理退休,养老金核算的这些知识要把握
- 量化|量化大师麦教授:美好的不确定性
- 浪胃仙|泡泡龙的离世给所有吃播提了醒,浪胃仙顺势决定“转行”,新职业认真的吗?
- 脑梗死|脑梗死和喝酒有没有关系呢?爱喝酒的朋友,应该看看
- 米歇尔·戴斯玛克特|海奥华预言的真相,地球人被带到九级文明,揭开神话背后的秘密
- 减肥也能吃的小零食,营养美味,低脂低热量,多吃也不怕!
- 1碗面粉,不加水,锅里蒸一蒸,做香甜可口的发糕,比蛋糕还香
- 扇贝最好吃的做法,适合冬日里吃,做法简单好吃不腻,家人超爱吃
- 七种颜色的布丁吃过没有?软糯爽口,Q弹软糯
- 爱吃南瓜饼的收藏,外酥里嫩,香甜软糯,饭桌上必备,做法超简单



















