数学|2020数学中考题分享之一:要正确作出辅助线并熟练运用垂径定理
文章图片

大家好 , 今天是2020年8月8日星期六 。 从今天开始 , 数学世界将持续给大家分享2020年各地的数学中考真题 , 这次分享一道2020年武汉数学中考题 , 希望能够对大家的学习有一些帮助!如果你是来到这里的新朋友 , 请翻看以前的文章 , 希望能够大家能够喜欢 。
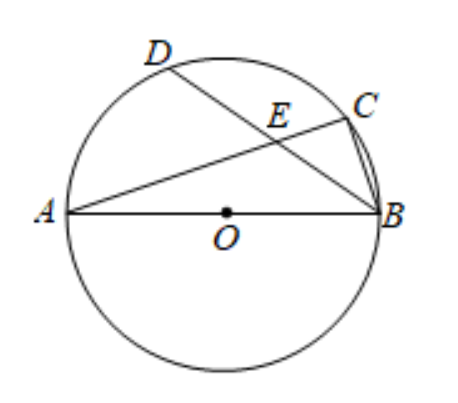
例题:(2020·武汉数学中考题)如图 , 在半径为3的⊙O中 , AB是直径 , AC是弦 , D是弧AC的中点 , AC与BD交于点E.若E是BD的中点 , 求线段AC的长 。
我们在做这道题时 , 要有效利用题中的已知条件 , 推出解决问题所需要的条件 , 同时要针对具体问题进行分析 , 并结合要求的结论进行思考 。 接下来 , 数学世界就与大家一起来完成这道例题吧!
分析:我们可以连接OD , 交AC于F , 根据垂径定理得出OD⊥AC , AF=CF , 再通过证明三角形全等得到DF=BC , 根据三角形中位线定理可以求得OF=1/2DF , 由于⊙O的半径为3 , 从而求得BC=DF=2 , 再利用勾股定理即可求得AC的长 。 下面 , 我们按照这个思路解答此题吧!
【数学|2020数学中考题分享之一:要正确作出辅助线并熟练运用垂径定理】
解答:连接OD , 交AC于F , (如图)
∵D是弧AC的中点 ,
∴OD⊥AC , AF=CF , (根据垂径定理)
∴∠DFE=90° ,
∵OA=OB , AF=CF ,
∴OF=1/2BC , (根据三角形中位线定理)
∵AB是直径 ,
∴∠ACB=90° ,
在△EFD和△ECB中 ,
∠DFE=∠ACB=90° ,
∠DEF=∠BEC ,
DE=BE ,
∴△EFD≌△ECB(AAS) ,
∴DF=BC ,
∴OF=1/2DF ,
∵OD=3 ,
∴OF+DF=3 ,
∴OF=1 ,
∴BC=2 ,
在Rt△ABC中 , AB=6 ,
AC^2=AB^2-BC^2 , (根据勾股定理)
∴AC=4√2 ,
即线段AC的长为4√2.
(完毕)
垂径定理:垂直于弦的直径平分弦 , 并且平分弦所对的劣弧、优弧 。
垂径定理的推论
平分弦(不是直径)的直径垂直于弦 , 并且平分弦所对的劣弧或优弧 。
平分弦所对的一条弧的直径垂直于弦并且平分弦所对的另一条弧 。
弦的垂直平分线经过圆心 , 并且平分弦所对的两条弦 。
这道题主要考查了圆中的垂径定理、三角形全等的判定和性质以及三角形中位线定理等 , 正确作出辅助线并能够熟练运用性质定理是解题的关键 。 温馨提示:朋友们如果有不明白之处或者有更好的解题方法 , 欢迎大家在下面留言讨论 。 谢谢!
推荐阅读
- 数学|你见过最讽刺的事是什么?信心满满把试卷给我抄成倒数第二!
- 清华大学|2020高考三大热门专业出炉,西科大成最大黑马,实力不输清华
- 西工大附中|2020年清北录取人数汇总,清华附中屈居第二,第三名是黑马
- 数学|事业单位又涨工资?除了它,这行也成“香饽饽”,工资不输公务员
- 教育厅|教育厅正式官宣!2020年复读生默泪,家长很无奈!
- 数学|我们一个被“嫌弃”了23年的数学天才,累死才知道他的价值
- 宁波诺丁汉大学|2020“最反常”大学,昔日录取线600分,如今只要400分,却没人报
- 厦门大学|2020“最惨”的1所985大学,2次征集志愿无果,考生:还真瞧不上
- 保研|2020保研率排名前50高校,北大成功过半,吉大上岸2000
- 钱钟书|他高考数学仅有15分,校长复查试卷后十分激动,道:就他了